Markov Chains Introduction

Markov Chains Introduction

A Markov Chain is a mathematical system that undergoes transitions from one state to another on a state space. It is a type of stochastic model, which means it involves randomness. To understand it from the ground up, we’ll look at its key features, how it works, and where it can be applied.

Key Features

• Memorylessness: This is the defining characteristic of a Markov Chain. It means that the next state depends only on the current state and not on the sequence of events that preceded it. This property is also known as the Markov Property.
• States: These are the various positions or conditions that the system can be in. A state in a Markov Chain captures all necessary information from the past to predict the future.
• Transitions: The movement from one state to another. Each transition has a probability associated with it, which is a measure of the likelihood of moving from one state to another.

How It Works

Imagine you have a simple weather model where the weather can be either sunny, cloudy or rainy on any given day. The weather of the next day depends only on the weather of the current day. You could represent this with a Markov Chain where the states are “sunny”, “cloudy” and “rainy”. The transitions between states are the probabilities of moving from one state to another - for example

t=0	t=1 odds	t=0	t=1 odds	t=0	t=1 odds
Sunny	0.7 sunny	Cloudy	0.2 sunny	Rainy	0.2 sunny
	0.2 cloudy		0.5 cloudy		0.2 cloudy
	0.1 rainy		0.3 rainy		0.6 rainy

What is probability it is sunny in 2 days when it is rainy today.

t=0: Rainy

t=1: 0.2 Sunny, 0.2 Cloudy, 0.6 Rainy

t=2: 0.2(0.7) + 0.2(0.2) + 0.6(0.2) = 0.14 + 0.04 + 0.12 = 0.3

$\therefore Probability=0.3$

Visual Representation

Markov Chains are often represented as a state diagram or a transition matrix:

• State Diagram: A graphical representation with circles for each state and arrows showing the transitions between states. The probabilities of transitioning are labeled on the arrows.
• Transition Matrix: A table where each cell [i, j] contains the probability of moving from state i to state j.

Suppose a discrete-time stochastic process is in one of s states.

A discrete-time stochastic process is a Markov Chain if

$$P({\text{X}}_{t+1}=i_{t+1}|{\text{X}}_t=i_t,{\text{X}}_{t-1}=i_{t-1},...,{\text{X}}_1=i_1,{\text{X}}_0=i_0)$$

for each time t = 0,1,2,… (i.e the chain is memoryless)

Stationarity Assumption

We further assume that $P({\text{X}}_{t+1}=j|{\text{X}}_t=i)$ is independent of t, so that we can write $P({\text{X}}_{t+1}=j|{\text{X}}_t=i)=p_{ij}$ which is called the transition probability from state i to state j

These probabilities populate a transition probability matrix P whose i-th row sum satisfies ${\Sigma }_{j=1}^s{p}_{ij}=1$ for all i = 1,2,…,s

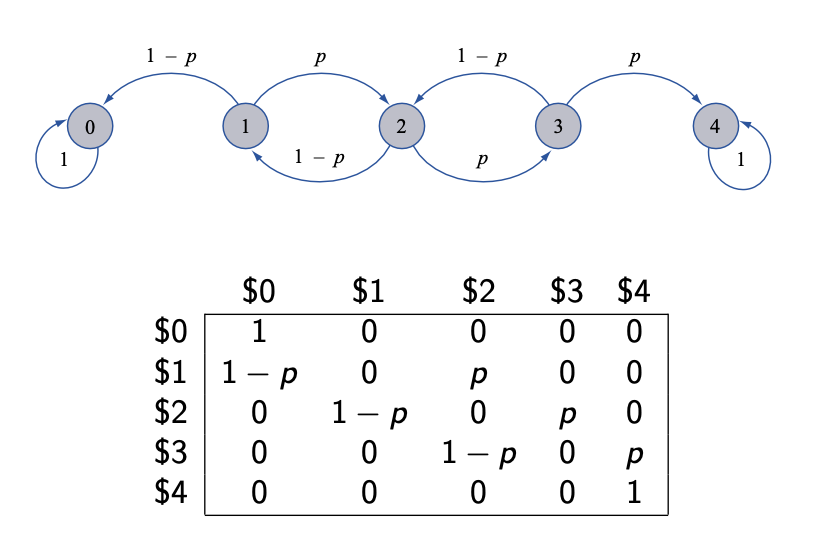
Example 1 - Gambler’s Ruin

t = 0: Suppose you have $2.

t = 1,2,3,… etc. Play a game in which you bet $1 each time.

In each game you either retain your betting dollar and win a additional dollar with probability p

or

You lose your betting dollar with probability 1-p

Goal: increase your capital to $4, when the sequence of games ends.

However, the sequence of games also ends if your capital is reduced to $0.

Let ${\text{X}}_0$ = initial capital and ${\text{X}}_t$ = capital after game t

Then ${\text{X}}_0,{\text{X}}_1,{\text{X}}_2,...$ is a discrete-time stochastic process.

Here ${\text{X}}_0=2$ is a constant but ${\text{X}}_1=3$ with probability p or ${\text{X}}_1=1$ with probability 1-p, and so on

Stopping conditions: if ${\text{X}}_t=4$ for some $t=t^{\ast }$, then ${\text{X}}_t=4\forall t\ge t^{\ast }$ Similarly, if ${\text{X}}_t=0$ for some $t=t^{\ast }$, then ${\text{X}}_t=0\forall t\ge t^{\ast }$