Newton Univariate Root Method

Newton Univariate Root Method

Aim:

• To find the root/s i.e where the function intercepts the x-axis

General Form:

• General formula for Newton’s Univariate Root approximation:

$$x^{k+1}=x^k-\frac{g(x^k)}{g^{\prime }(x^k)}$$

from sympy import symbols, diff, lambdify, parse_expr
 
x = symbols('x')
 
def newton_uni_root_method(f_sym, x0, tolerance=0.0005, max_iterations=100):
 
	# Convert symbolic function to a numerical function
	f = lambdify(x, f_sym, 'numpy')
	df_sym = diff(f_sym, x)
	df = lambdify(x, df_sym, 'numpy')
 
	results = []
	k = 0
	xk = x0
 
while k < max_iterations:
	f_xk = f(xk)
	df_xk = df(xk)
 
 
	# Avoid division by zero
	if df_xk == 0:
		raise ValueError(f"Zero derivative. No solution found at x = {xn}")
 
	# Newton univariate method update
	delta = - f_xk / df_xk
	xk1 = xk + delta
 
	results.append((k, xk, f_xk, df_xk, delta, xk1))
 
	if abs(xk1 - xk) < tolerance:
		break
 
	xk = xk1
	k += 1
 
	return results

Example

$$f(x)=1+2x^2-e^x$$

with initial guess

$$x=0.8$$

which is a decent guess looking at the plot of the function

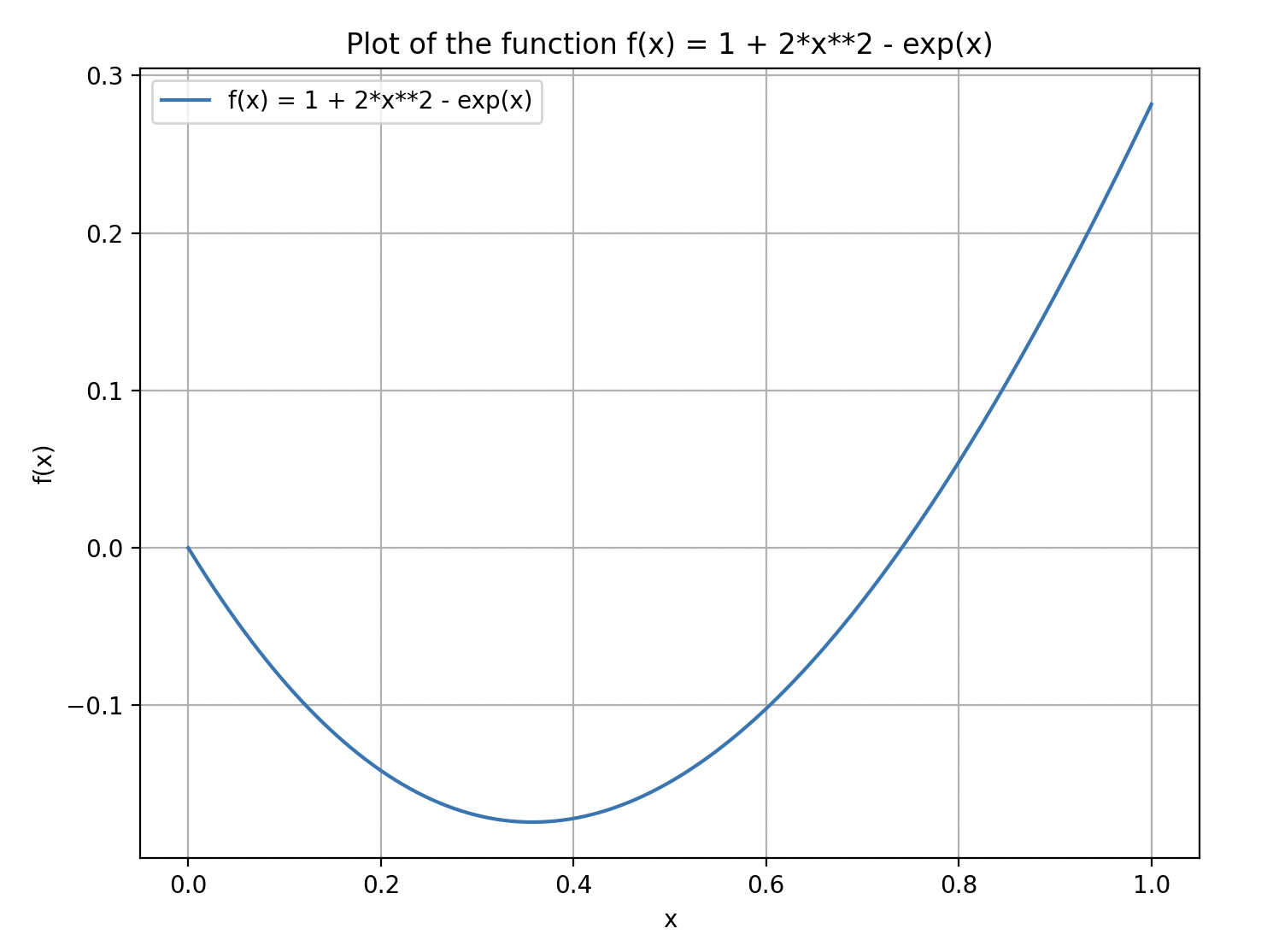The x-intercepts of the function will be at x = 0 and another x-value somewhere between 0.6 and 0.8

Following the algorithm for newton univariate roots, we can tabulate the key values in a table as follows

$k$	$x^k$	$f(x^k)$	$f^{\prime }(x^k)$	$\Delta (x^k)$
0	0.8	0.054 459	0.974 459	-0.055 886
1	0.744 114	0.002 835	0.871 879	-0.003252
2	0.740 862	0.000 010	0.865 705	-0.000 012
3	0.740 850	-	-	-
using a tolerance of 0.0005 to stop the algorithm results in $x^{\ast }\approx 0.740850$
Next we’re going to look at Newton Univariate Method