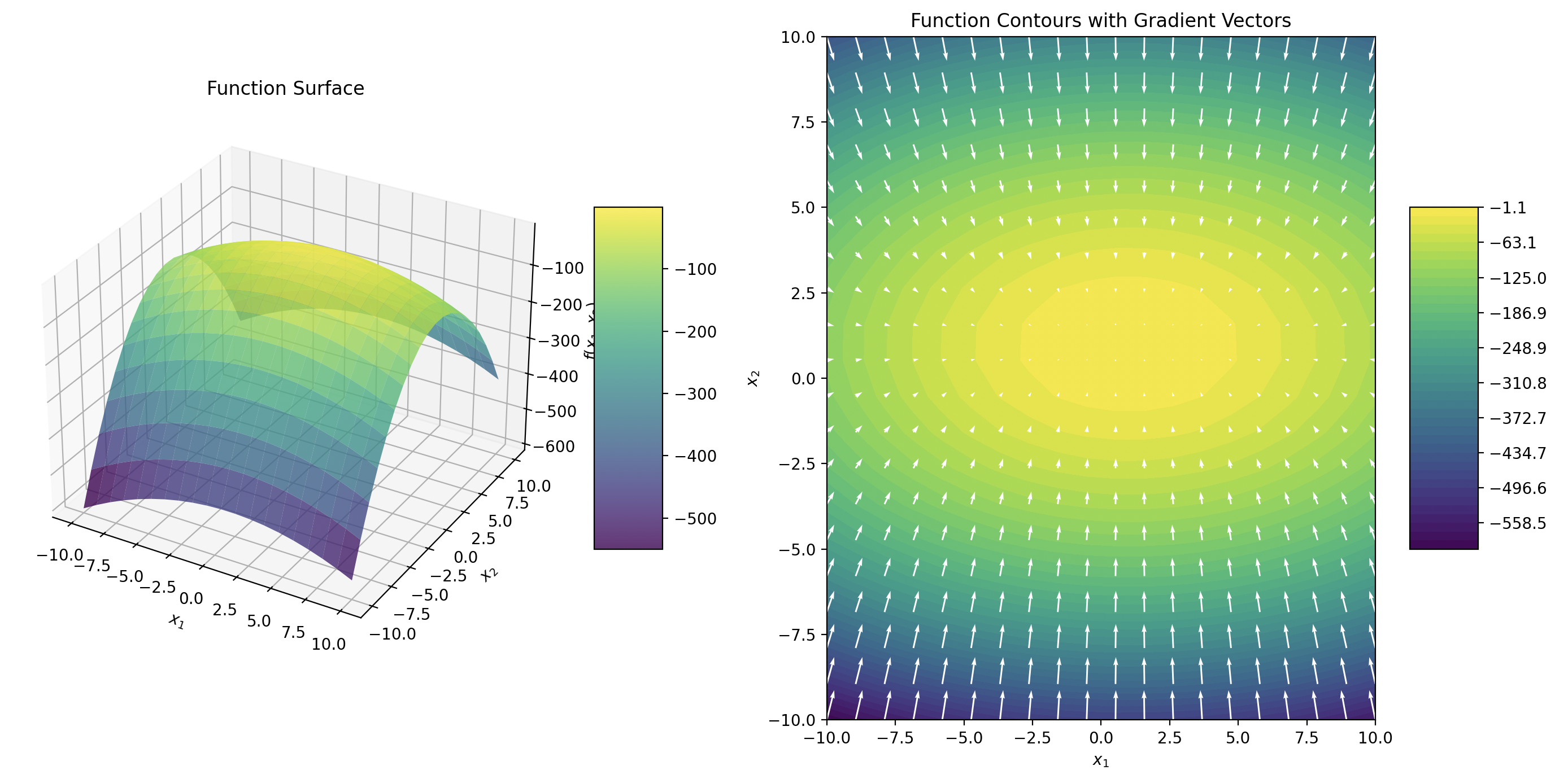
Method of Gradient Ascent
Similar to Method of Gradient Descent Also see Gradient Ascent

Consider the function
with initial estimate
Calculate the gradient vector
and the Hessian Matrix
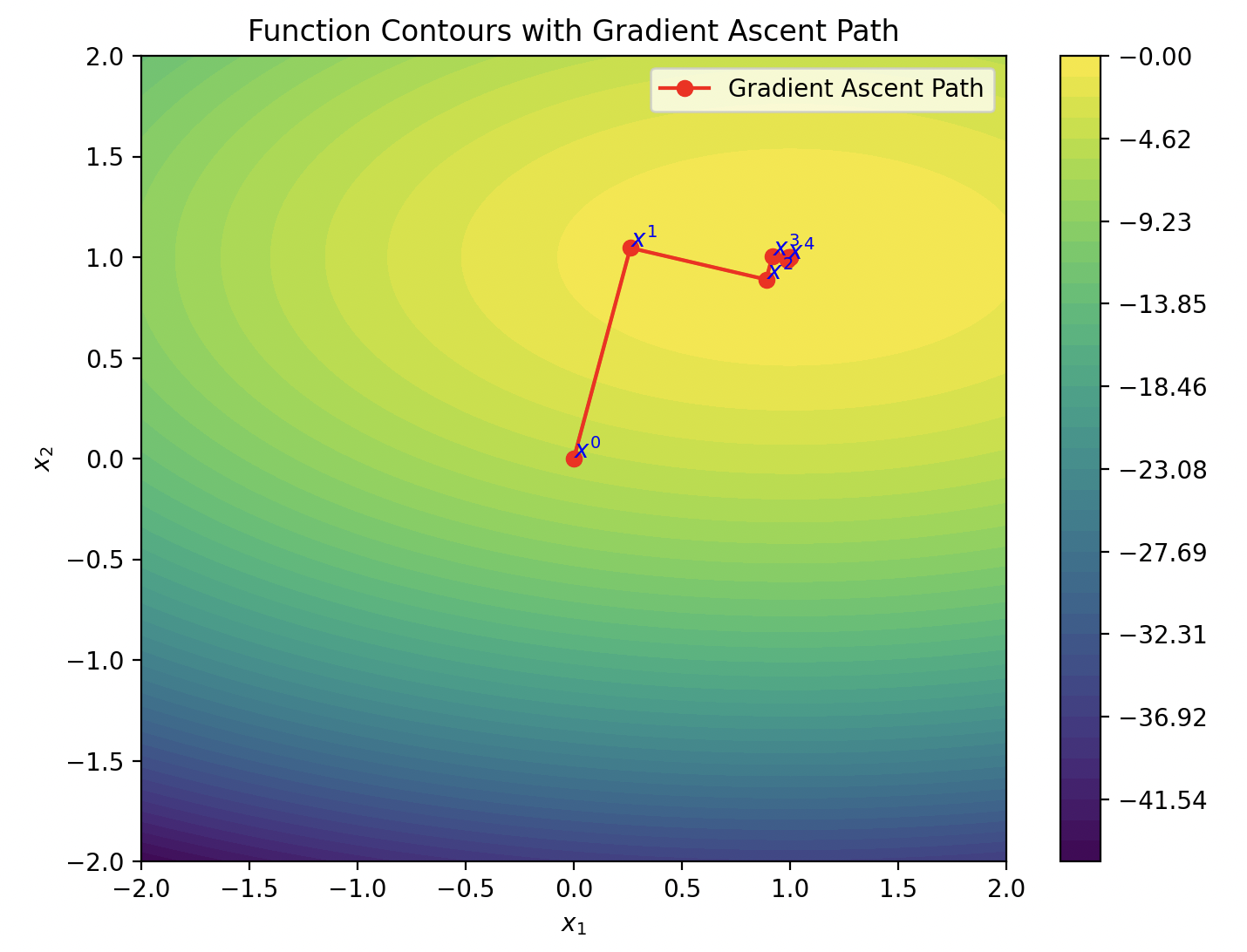
Look at the plot
Do one step of gradient ascent:
The general gradient ascent algorithm for any function with a maximum.
def gradient_ascent(func, x0):
"""
Performs one step of gradient ascent with optimal alpha calculation
for a given sympy function of x1 and x2, starting from x0.
Parameters:
- func: sympy function of two variables, x1 and x2.
- x0: Initial point as a list or tuple of two numbers [x1, x2].
Returns:
- New point as a list [x1, x2] after one step of gradient ascent.
- Optimal alpha used for the step.
"""
# Define symbols
x1, x2, alpha = symbols('x1 x2 alpha')
# Calculate gradient
grad = [diff(func, var) for var in [x1, x2]]
# Substitute x0 into gradient and express new point as function of alpha
grad_at_x0 = [g.subs([(x1, x0[0]), (x2, x0[1])]) for g in grad]
x1_new = x0[0] + alpha * grad_at_x0[0]
x2_new = x0[1] + alpha * grad_at_x0[1]
# Function value as a function of alpha
f_alpha = func.subs([(x1, x1_new), (x2, x2_new)])
# Derivative of function with respect to alpha and solve for optimal alpha
df_dalpha = diff(f_alpha, alpha)
optimal_alpha_solution = solve(df_dalpha, alpha)
# Handle multiple solutions for alpha
if not optimal_alpha_solution:
print("No solution found for alpha. Check the function's form.")
return x0, None # Return original point and None for alpha if no solution
optimal_alpha = optimal_alpha_solution[0] # Assuming the first solution is optimal
# Calculate new point using the optimal alpha
x1_optimal = x1_new.subs(alpha, optimal_alpha)
x2_optimal = x2_new.subs(alpha, optimal_alpha)
return [x1_optimal, x2_optimal], optimal_alpha# Example of usage with a symbolic function
x1, x2 = symbols('x1 x2')
func = -x1**2 - 4*x2**2 + 2*x1 + 8*x2 - 5 # Example function
x0 = [0, 0] # Initial point
new_point, optimal_alpha = gradient_ascent(func, x0)
print(f"New point: {new_point}")
print(f"Optimal alpha: {optimal_alpha}")For the function considered, this code will return
which will result in the next estimate
Continue doing gradient ascent steps until it converges to the approximate global maximum